

숫자를 0과 1로만 나타내는 것이 이진법입니다.




진법 이해하기
십진법 숫자 1234를 봅시다.
자릿수별로 떼어서 보면, 1000 * 1 + 100 * 2 + 10 * 3 + 10 * 4이죠?
이는 곧 103 * 1 + 102 * 2 + 101 * 3 + 100 * 4와 같습니다.
자릿수간에 10배 차이가 나죠.
n개의 자릿수 차이가 나면 10n배 차이가 나게 됩니다.
a진법을 구성하는 방법이 이런 겁니다.
각 자릿수의 수를 c0, c1, c2, ⋯ 라 하면
a진법 수는 a0 * c0 + a1 * c1 + a2 * c2 + a3 * c3 + ⋯ + an * cn와 같이 표현됩니다.
자릿수간엔 a배 차이가 나죠.
n개의 자릿수 차이가 나면 an배 차이가 나게 됩니다.
기호들이 많아서 눈에 안 들어오실 수도 있겠지만 크게 어렵지 않은 내용입니다.
평소에 1000의 자리, 100의 자리, 10의 자리, 1의 자리라고 부르던 것을
103의 자리, 102의 자리, 101의 자리, 100의 자리라고 새로이 부르면 바로 이해할 수 있으니까요.
이진법 ↔ 십진법 변환하기
먼저 이진법 수를 십진법으로 변환하는 것부터 보겠습니다.
간단합니다.
위에서 본 진법의 구성 원리대로 이진법 수를 표현하고, 덧셈을 완료해주면 됩니다.
- 1001000(2) = 26 * 1 + 25 * 0 + 24 * 0 + 23 * 1 + 22 * 0 + 21 * 0 + 20 * 0
= 26 * 1 + 23 * 1 = 64 + 8 = 72 - 1101001(2) = 26 * 1 + 25 * 1 + 24 * 0 + 23 * 1 + 22 * 0 + 21 * 0 + 20 * 1
= 26 * 1 + 25 * 1 + 23 * 1 + 20 * 1 = 64 + 32 + 8 + 1 = 105
숫자 아래에 자릿수에 해당하는 수를 표시하면 훨씬 쉽게 할 수 있습니다.
- 1 0 0 1 0 0 0
64 32 16 8 4 2 1
64 + 8 = 72 - 1 1 0 1 0 0 1
64 32 16 8 4 2 1
64 + 32 + 8 + 1 = 105
십진수를 이진수로 변환하는 법은, 수를 계속해서 2로 나눈 뒤 그 나머지를 역순으로 배치하는 겁니다.
2 │72
2 │36 ⋯ 0
2 │18 ⋯ 0
2 │9 ⋯ 0
2 │4 ⋯ 1
2 │2 ⋯ 0
1 ⋯ 0
72 = 1001000(2)
2 │105
2 │52 ⋯ 1
2 │26 ⋯ 0
2 │13 ⋯ 0
2 │6 ⋯ 1
2 │3 ⋯ 0
1 ⋯ 1
105 = 1101001(2)
이게 정말 제대로된 원리에 따른 것일까 하고 의문을 가지고 계신 분은
사실 이 과정이 아래 과정을 따라간 것이라고 생각하시면 됩니다.
105 = 104 + 1 = 21 * 52 + 20 * 1 = 22 * 26 + 20 * 1 = 23 * 13 + 20 * 1 = 23 * (12 + 1) + 20 * 1 = 24 * 6 + 23 * 1 + 20 * 1
= 25 * 3 + 23 * 1 + 20 * 1 = 25 * (2 + 1) + 23 * 1 + 20 * 1 = 26 * 1 + 25 * 1 + 23 * 1 + 20 * 1

컴퓨터와 이진법
오늘날의 컴퓨터는 트랜지스터가 집적된 IC회로를 통해 정보를 저장합니다.
핵심은 트랜지스터인데요.
트랜지스터는 일정 전압을 기준으로 그보다 더 큰 전압은 증폭시키고, 더 작은 전압은 소멸시키는 일종의 스위칭 작용을 합니다.
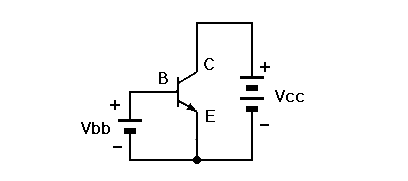
그래서 신호는 증폭되는 신호, 소멸되는 신호로 구분되고 이를 통해 0과 1로 구성된 신호를 구현하는 것이죠.
컴퓨터가 이진법을 채택한 역사는 컴퓨터가 트랜지스터를 사용한 역사보다 길기 때문에,
트랜지스터를 이용하기 때문에 이진법을 사용한다는 틀린 말이 되겠습니다.
컴퓨터가 이진법을 이용하는 점이 트랜지스터의 특성과 잘 맞아떨어진 것이죠.
컴퓨터가 이진법을 사용하는 이유는 True/False의 두 가지 값이 있을 때가 제일 논리 회로를 구성하기 쉽고,
현실 세계에서 전기 신호는 변동폭이 있는데, 구분해야 하는 신호의 종류가 단 두 가지만 있는 편이 오류율이 적기 때문입니다.
이진법에 대한 정보는 도움이 되었나요?
이진법은 기초적인 내용이라 전공하는 사람들 보다는 취미로 혹은 별 생각 없이 찾아본 사람들이 더 많을 것 같은데,
너무 정석적으로 설명하다보니 쉬운 글은 못 된 것 같습니다.
그래도 이런 걸 눈에 익히는 편이 무의식적으로 훨씬 기억에 남을 거에요!
'Computer Science' 카테고리의 다른 글
| [CS] 이진수로 소수를 나타내는 법 (0) | 2022.07.09 |
|---|---|
| [CS] 덧셈밖에 못하는 컴퓨터가 어떻게 2의 보수를 이용해 뺄셈을 할까요? (0) | 2022.07.08 |
| [CS] 비트와 바이트의 차이, 그리고 KB/MB/GB/TB (0) | 2022.07.07 |
![[CS] 이진법과 십진법 사이 변환하기, 컴퓨터와 이진법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fc4m19P%2FbtrGElB4HKy%2FauV2zx4XT54MyJdPKYFkdK%2Fimg.png)