
다양한 자료형 글에서, 자료형들의 최댓값과 최솟값을 알아보셨습니다.
변수에 자료형의 최댓값보다 큰 수를 넣거나 자료형의 최솟값보다 작은 수를 넣으면 어떻게 될까요?
호기심이 생기지 않나요?

자료형의 표현 한계를 넘는 값을 저장하려 하면
오버플로우, 언더플로우, 랩 어라운드 중 하나가 발생합니다.




산술 오버플로우
변수를 상자에 비유하는 책이 많습니다.
상자가 물건을 담는 공간이듯이, 변수도 값을 담는 공간이죠.
어떤 값을 담는 변수인지, 상자의 종류를 나타내는 것이 자료형이고요.
그런데 최근에 저는 제 친구에게서 흥미로운 비유를 들었습니다.
변수를 상자보다 컵에 비유하더군요.
컵이 액체를 담듯이, 변수도 값을 담는 겁니다.
와인잔인지, 맥주잔인지, 소주잔인지, 종이컵인지 그 컵의 종류에 해당하는 게 자료형이고요.
그리고 컵이 꽉 찼는데 액체를 더 담으려 하면, 액체가 넘쳐(over) 흐릅니다.(flow)
확실히 컵에 비유를 하니, overflow가 어떤 것일지 확 와닿습니다.
아직 설명은 안 했지만, 여러분들도 감이 오시죠?
변수도 컵처럼, 한계를 넘어서 값을 담으면 넘쳐 흐릅니다.
어떻게요?
부호가 바뀌어 버립니다.
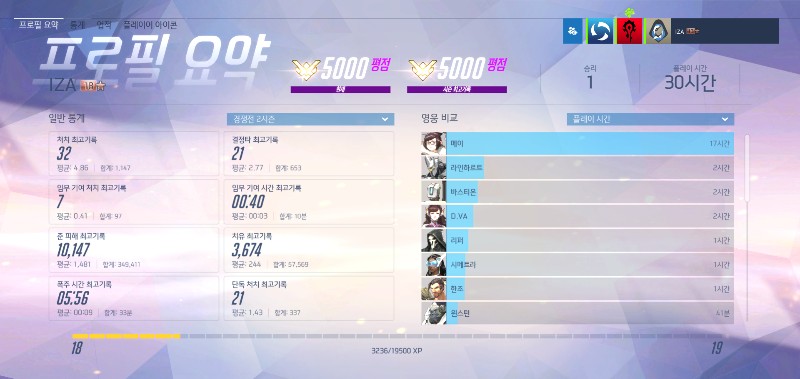
게임 오버워치에서 예전에 일어난 일입니다.
승률이 0%인 유저가 어느날 갑자기 랭킹 1등으로 등극해버립니다.
그것도 말도 안되는 5000점이라는 점수와 함께 말이죠.
어떻게 승률이 0%인데 랭킹 1등이 될 수 있었을까요?
그 진실은 이렇습니다.
이 유저는 점수가 0점에 한없이 가까웠고, 한 번만 더 패배를 한다면 점수가 음수가 되어버리는 상황이었습니다.
그런데 실제 게임에서 점수의 표현 범위는 0~5000 이었고, -10이나 -20같은 숫자를 표현할 순 없었죠.
그래서 마치 순환 열차처럼, 0에서 더 내려가니 갑자기 5000이 튀어나와 버린 겁니다.
이것은 사실 오버플로우는 아니고, 뒤에서 알아볼 랩 어라운드(wrap around)에 해당하는 예시입니다.
하지만 제일 먼저 이야기하는 편이 이 사례가 오버플로우나 언더플로우의 사례라는 통념도 깨고 좋겠죠.
우리가 이번 글에서 알아볼 모든 것들이 다 이 상황과 유사합니다.

이번 소스의 이름은 "4. 오버플로우, 언더플로우, 랩어라운드.c" 라고 지었습니다.
|
#include <stdio.h>
#include <limits.h>
int main()
{
int overflow = INT_MAX + 1;
printf("overflow : %d\n", overflow);
return 0;
}
|
cs |
위 코드를 그대로 적어서 실행시켜주세요.
overflow라는 이름의 변수에는 INT_MAX + 1이란 값이 들어갔습니다.
최댓값 + 1이 어떤 값을 나타내나 호기심이 생겨 실험한 것이죠.
실행시켜보면,

부호가 바뀌어있습니다.
숫자는 뭔가 익숙한 숫자죠.
21억, 감이 좋으시다면 왠지 int의 최솟값과 비교해 보고 싶은 마음이 드실 겁니다.
그래서 한 줄을 추가해봅니다.
|
#include <stdio.h>
#include <limits.h>
int main()
{
int overflow = INT_MAX + 1;
printf("overflow : %d\n", overflow);
printf("INT_MIN : %d\n", INT_MIN);
return 0;
}
|
cs |
그리고 실행시켜보면,

신기하게도 두 값이 같습니다!
최댓값 + 1을 했더니 최솟값이 튀어나오네요!
여러분의 마음 속에선 한 가지 호기심이 더 자라났습니다.
바로, 최솟값 - 1은 최댓값과 같을까 하는 것이죠.
또 코드를 추가해봅시다.
|
#include <stdio.h>
#include <limits.h>
int main()
{
int overflow = INT_MAX + 1;
printf("overflow : %d\n", overflow);
printf("INT_MIN : %d\n", INT_MIN);
int overflow2 = INT_MIN - 1;
printf("overflow2 : %d\n", overflow2);
printf("INT_MAX : %d\n", INT_MAX);
return 0;
}
|
cs |
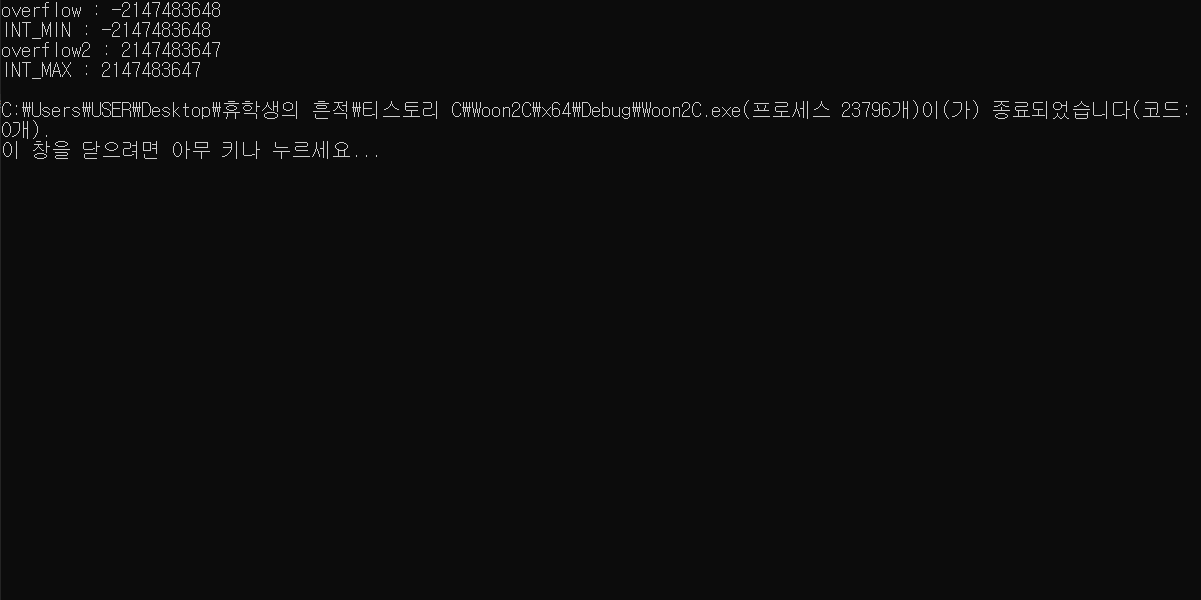
어떤가요, INT_MIN - 1과 INT_MAX가 같은 값이죠?
최솟값 - 1은 최댓값과 같습니다!
표현 범위 내에서 값이 순환한다고 생각할 수 있겠습니다.
그림으로 나타내보면,
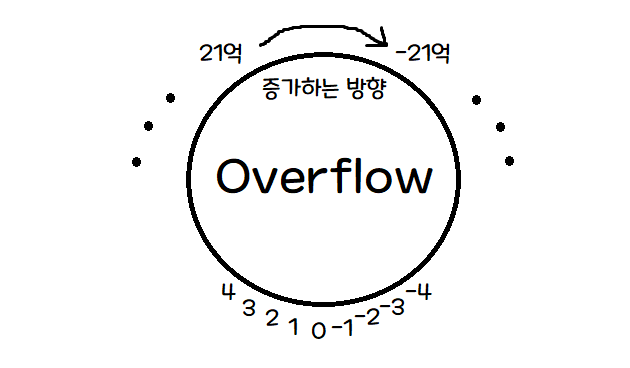
이런 느낌인 거죠.
그렇다면 최댓값 + 1을 해서 최솟값이 되는 것이 오버플로우고,
최솟값 - 1을 해서 최댓값이 되는 것이 언더플로우인가요?
아니요.
아니요.
아니요!
오버플로우, 더 정확하게는 산술 오버플로우(arithmetic overflow)는 말이죠.
"표현 한계를 넘어 부호가 바뀌는 상황"을 말합니다.
컴퓨터가 부호 있는 2진수 정수를 저장할 때 최상위 비트는 부호 비트이고 나머지 비트들이 값을 나타내는 비트들인데,
값의 절댓값이 너무 커져서 부호 비트까지 침범하게 되면 부호가 바뀝니다.
이 상황을 산술 오버플로우라고 부릅니다.
부호 있는 2진수 정수라고 한정했죠?
unsigned int나 float에서도 비슷한 일들이 일어납니다.
최댓값보다 커지면 최솟값이 등장하고, 최솟값보다 작아지면 최댓값이 등장하죠.
이 상황들을 부르는 명칭은 또 따로 있습니다.
뒤 항목에서 볼 내용들이죠.
첫 번째 항목을 확실하게 정리합시다.
산술 오버플로우는 부호 있는 정수 타입에서, 표현 한계를 넘어 부호가 바뀌는 상황을 일컫습니다.
아래 글에서 산술 오버플로우라고 불리는 개념이 등장한 배경을 알 수 있습니다.
https://jartlife.tistory.com/113?category=985134
[CS] 덧셈밖에 못하는 컴퓨터가 어떻게 2의 보수를 이용해 뺄셈을 할까요?
우리는 컴퓨터로 사칙연산과 복잡한 미적분까지 계산하지만, 근본적으로 컴퓨터는 덧셈밖에 하지 못 합니다. 멀리까지 가진 말고, 덧셈밖에 못하는 컴퓨터는 어떻게 뺄셈을 하는지 알아봅시다.
jartlife.tistory.com
랩 어라운드
다음으로 소개할 것은 랩 어라운드(wrap around)입니다.
게임 오버워치에서 승률 0%인 유저가 랭킹 1등에 등극해버린 사건, 바로 그 사건에서 발생한 일이지요.
산술 오버플로우와 아주 유사해서 내용은 짧을 것 같습니다.
산술 오버플로우는 부호 있는 정수에서 부호가 바뀌는 것이었죠?
랩 어라운드는, 부호 없는 정수에서 최댓값 + 1을 하면 최솟값이 나오고, 최솟값 - 1을 하면 최댓값이 나오는 상황입니다.
|
#include <stdio.h>
#include <limits.h>
int main()
{
int overflow = INT_MAX + 1;
printf("overflow : %d\n", overflow);
printf("INT_MIN : %d\n", INT_MIN);
int overflow2 = INT_MIN - 1;
printf("overflow2 : %d\n", overflow2);
printf("INT_MAX : %d\n", INT_MAX);
unsigned wrap_around = UINT_MAX + 1;
printf("wrap_around : %u\n", wrap_around);
unsigned wrap_around2 = -1;
printf("wrap_around2 : %u\n", wrap_around2);
printf("UINT_MAX : %u\n", UINT_MAX);
return 0;
}
|
cs |
코드는 위와 같이 늘어났습니다.
unsigned int의 최솟값은 0이라서, UINT_MIN은 따로 존재하지 않는다는 점, 알아두시구요!
최댓값 + 1을 unsinged int에 넣었을 때 0이 나오고,
-1을 unsigned int에 넣었을 때 최댓값이 나오기를 기대합니다.
결과는요?
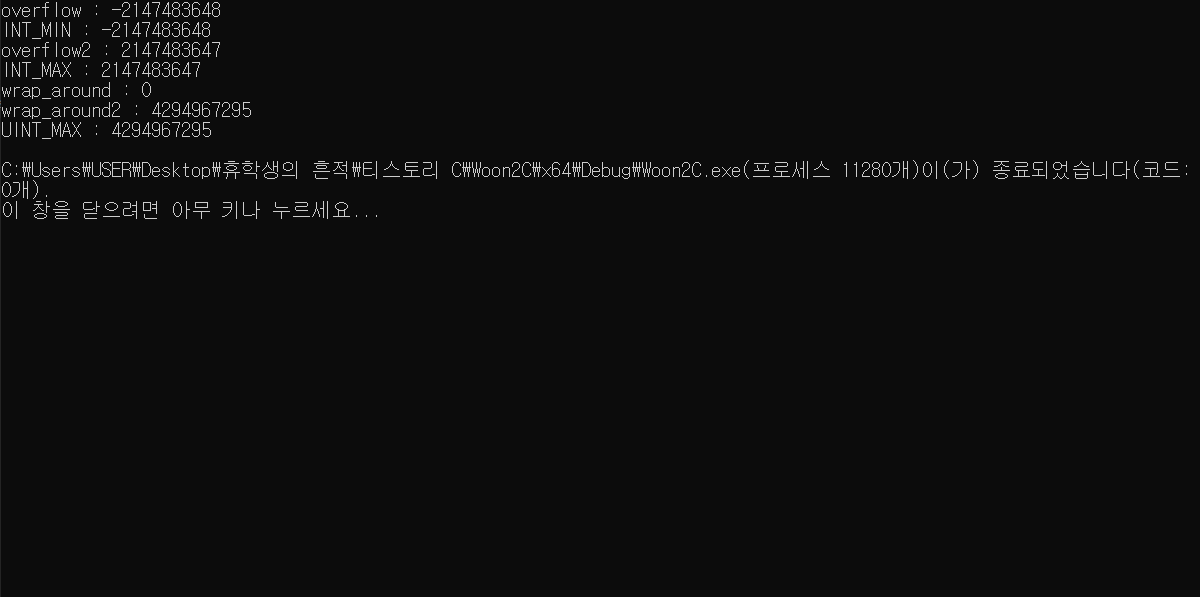
네, 우리가 기대했던 대로입니다.
부호 없는 정수는 부호 비트가 따로 존재하지 않습니다.
따라서 부호가 바뀌는 상황에 해당하는 산술 오버플로우는 부호 없는 정수에 적용되지 않습니다.
2진수 정수의 최상위 비트가 1이었는데, 1+1=2로 자리 올림이 발생하면 최상위 비트는 0으로 세팅되죠.
최상위 비트보다 상위의 비트는 존재하지 않기 때문에 발생한 올림수는 그냥 버려지게 됩니다.
예를 들어 11111111(2) + 00000001(2)는 본래 100000000(2)여야 하지만 8비트 정수에서 9비트째에 해당하는 1은 표현할 수가 없죠.
따라서 이 1을 그냥 버리게 되면 00000000(2)가 되는 겁니다.
자 그럼 랩 어라운드도 정리해봅시다.
랩 어라운드는, 부호 없는 정수에서 최댓값 + 1을 하면 최솟값이 나오고, 최솟값 - 1을 하면 최댓값이 나오는 상황을 일컫습니다.

언더플로우
언더플로우(underflow)는 그럼 대체 어떤 상황일까요?
언더플로우 개념은 부동소수점 자료형에 대해 완벽한 이해를 요구합니다.
하지만 이 글에서 거기까지 다루기엔 너무 멀리 간 주제 같군요.
그래서 이렇게 설명해보려 합니다.
일종의 규약(IEEE 754)에 의해 실수 자료의 표현은 과학적 표기법과 유사합니다.
과학적 표기법과 정밀도, 정규화에 대한 개념이 있으시다면 더 편하게 읽으실 수 있을 겁니다.
모든 숫자를 1.02754 * 104와 같이 1.xxx * 10x로 표현하는 것이 과학적 표기법입니다.
컴퓨터는 2진수를 사용하죠?
그래서 실수를 나타낼 때는 모든 수를 1.xxx * 2x로 표현하기로 약속합니다.
숫자의 정밀도는 소수 자리수가 얼마나 많은가, 숫자의 크기는 2의 지수가 얼마나 큰가로 결정됩니다.
부동소수점 자료형에서, 지수 부분이 너무 크다면, 무한(infinity)으로 표기하는데, 이것이 지수 오버플로우(exponent overflow)입니다.
반대로 지수 부분이 너무 작다면, 0으로 표기하는데, 이것이 지수 언더플로우(exponent underflow)입니다.
부호는 전혀 상관이 없고, 지수 부분의 크기만을 기준으로 합니다.
예를 들어 0.000000001(10)이나 -0.000000001(10)이나 굉장히 작은 절댓값을 가지고 있죠.
이들을 1.xxx * 2x꼴로 표현하려면 굉장히 작은(절댓값이 매우 큰 음수인) 지수가 필요합니다.
그런데 이렇게 작은 지수를 표현하기 위한 비트 수가 모자라다면, 지수 언더플로우입니다.
모든 비트를 0으로 세팅하게 되죠.
사실은 지수 부분이 모자라더라도 최대한 표현하기 위해서 조금의 노력을 더 하긴 합니다만, 이렇게 알고 계셔도 큰 문제가 없습니다.
이 부분이 더 궁금하시다면 IEEE754를 참고하세요.
|
#include <stdio.h>
#include <limits.h>
int main()
{
int overflow = INT_MAX + 1;
printf("overflow : %d\n", overflow);
printf("INT_MIN : %d\n", INT_MIN);
int overflow2 = INT_MIN - 1;
printf("overflow2 : %d\n", overflow2);
printf("INT_MAX : %d\n", INT_MAX);
unsigned wrap_around = UINT_MAX + 1;
printf("wrap_around : %u\n", wrap_around);
unsigned wrap_around2 = -1;
printf("wrap_around2 : %u\n", wrap_around2);
printf("UINT_MAX : %u\n", UINT_MAX);
float underflow = 0.000000001f;
printf("underflow : %f\n", underflow);
return 0;
}
|
cs |
underflow 변수를 추가했습니다. 매우 작은 수를 저장하죠.
뒤에 f라는 접미사가 붙는데, 그냥 0.000000001은 컴퓨터가 float 타입의 상수라 인식하지 않고 double 타입의 상수라 인식하기 때문입니다.
float타입이니까, f를 붙여서 float 타입임을 나타내는 것이죠.
리터럴 상수와 접미사를 다루는 글에서 다시 다룰 내용입니다.
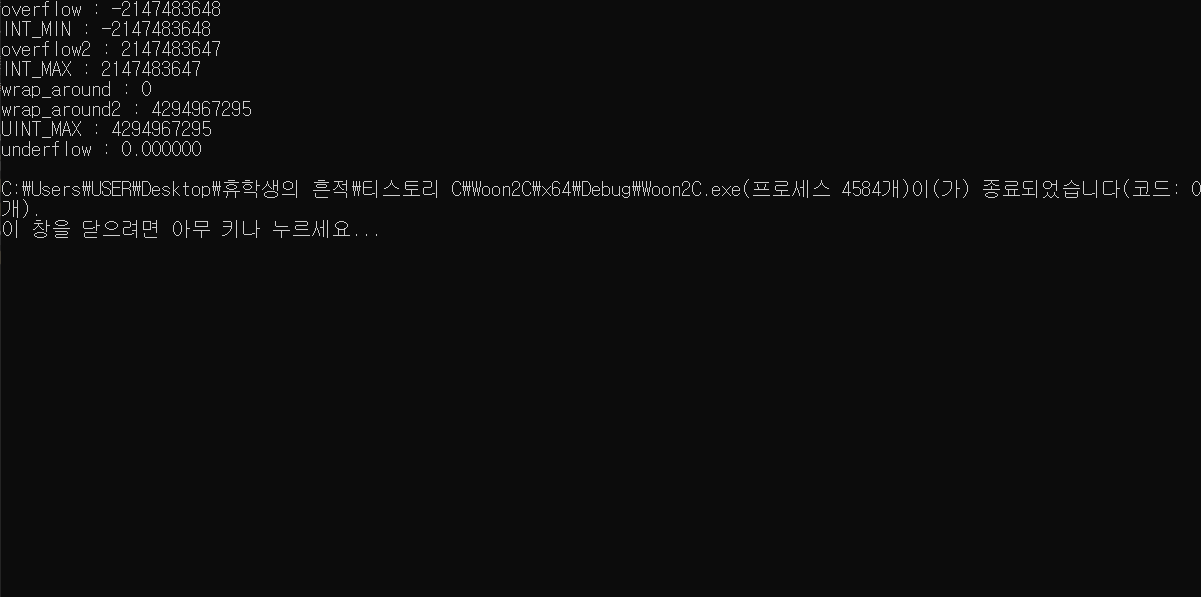
실행 결과는 위와 같습니다.
소수 9번째 자리수인 1은 온데간데 없이 0이 출력되었죠.
지수 언더플로우가 발생하였습니다.
언더플로우라고 부르는 상황이 한 가지 더 있습니다.
정수와 달리 실수는 수와 수의 간격이 무한히 좁잖아요?
소수 자리수는 무한하죠.
하지만 컴퓨터가 표현할 수 있는 소수 자리수에는 한계가 있습니다.
정밀도가 매우 높은 수를 표현하려 하면, 필연적으로 비트가 모자라게 됩니다.
숫자의 크기와는 상관 없이, 얼마나 정밀하냐(유효숫자가 몇 개이냐)에 의해 결정되는 일이죠.
|
#include <stdio.h>
#include <limits.h>
int main()
{
int overflow = INT_MAX + 1;
printf("overflow : %d\n", overflow);
printf("INT_MIN : %d\n", INT_MIN);
int overflow2 = INT_MIN - 1;
printf("overflow2 : %d\n", overflow2);
printf("INT_MAX : %d\n", INT_MAX);
unsigned wrap_around = UINT_MAX + 1;
printf("wrap_around : %u\n", wrap_around);
unsigned wrap_around2 = -1;
printf("wrap_around2 : %u\n", wrap_around2);
printf("UINT_MAX : %u\n", UINT_MAX);
float underflow = 0.000000001f;
printf("underflow : %f\n", underflow);
float underflow2 = 1234567.89f;
printf("underflow2 : %f\n", underflow2);
return 0;
}
|
cs |
1234567.89가 그대로 저장되는지 한번 볼까요?

저런!
1234567.89가 어느새 1234567.875로 변해있습니다.
언더플로우가 발생하였죠.
몇몇 분들은 오히려 소수 자릿수가 늘어났는데 뭔가 이상하지 않나요? 라고 하실 수 있습니다.
눈치가 좋고 아주 좋은 호기심입니다.
지금 우리가 보고 있는 숫자들이 실제로는 2진수로 저장된다는 점에 열쇠가 있습니다.
0.875만 따로 떼서 생각해봅시다.
0.875는 0.125*7로, 111(2)*2-3입니다.
0.89에 좀 더 가까이 근사시키려면요?
111001(2)*2-6 = 0.890625(10)으로 좀 더 0.89에 가까워졌습니다.
정밀도가 세 자리 증가하였죠.
0.89에 더 가깝게 표현할 수 있는 방법이 있음에도 불구하고 그렇지 못했습니다.
바로, 정밀도에 한계가 왔다는 소리죠.
그래서 0.89는 0.875가 된 겁니다.
지수 언더플로우를 마주할 일은 거의 없으시겠지만,
이 언더플로우 상황은 실제로 프로젝트를 하시다 보면 엄청나게 많이 마주하시게 될 겁니다.
물리 엔진이 잘 돌아가다가 갑자기 심각하게 삐끗거린다면 대부분 이 작은 오차들이 누적된 것이죠.
프로젝트 뿐만일까요, 아마 여러분들이 전공생이시라면
적어도 한 번은 교수님께서 이 문제로 골머리를 앓게 할 과제를 내주실 겁니다.
그러니 꼭 기억해두셨다가 부동소수점 자료 관련 애로사항을 마주쳤을 때 이 내용을 떠올리시기 바랍니다.
컴퓨터가 저장할 수 있는 부동소수점 자료의 정밀도에는 한계가 있습니다.
그리고 언젠가, 머신 엡실론(machine epsilon)이라는 단어를 검색해서 그 해결 방법을 찾아보시기 바랍니다.
자, 어려운 내용들은 다 지나왔습니다.
이쪽은 단순 코딩보다는 컴퓨터공학 쪽에 훨씬 가까운 내용이기 때문에 난이도가 훨씬 어려웠죠.
나중에 소개해드려도 되는 내용이었습니다만은,
제가 생각하기에 변수와 관련된 내용은 아예 처음부터 깊게 잡고 가는 게 훨씬 더 도움이 될 것 같았습니다.
그럼, 긴 글 읽느라 수고하셨습니다!
다음엔 조금 더 짧은 글로 뵈어요~

'C | C++ > C' 카테고리의 다른 글
| [C] 6. printf를 좀 더 잘 써봅시다. <필드폭 및 소수점 조정, 이스케이프 문자> (1) | 2022.07.05 |
|---|---|
| [C] 5. 입출력은 프로그램의 근본입니다. <printf, scanf> (0) | 2022.07.05 |
| [C] 3. 좀 더 다양한 종류의 변수를 선언해봅시다. <다양한 자료형> (0) | 2022.06.25 |
| [C] 2. 올바른 이름을 적읍시다. <변수의 이름 규칙> (0) | 2022.06.25 |
| [C] 1. 처음은 변수를 만들어보는 것으로 시작합시다. <변수 선언, 초기화> (0) | 2022.06.10 |
![[C] 4. 변수의 최댓값을 넘기면 무슨 일이 일어날까요? <오버플로우, 언더플로우, 랩 어라운드>](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fdi2ZUV%2FbtrGjc0StJa%2Fh8wnSF4bjffkSOjCIOPQ9K%2Fimg.png)